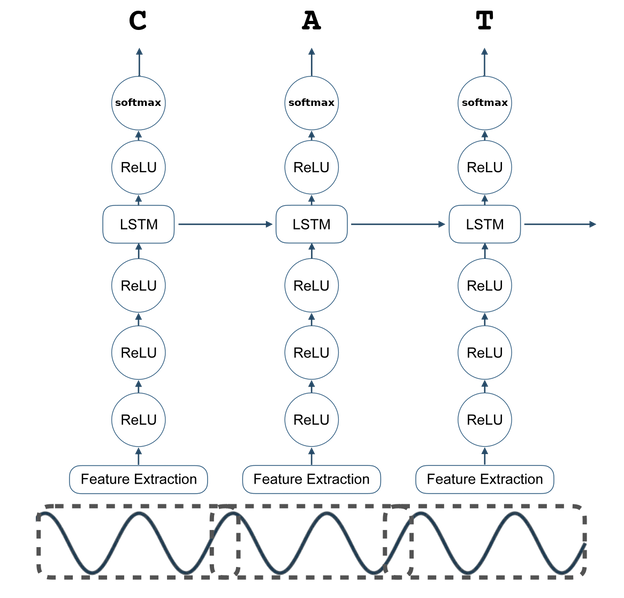
DeepSpeech Model¶
The aim of this project is to create a simple, open, and ubiquitous speech recognition engine. Simple, in that the engine should not require server-class hardware to execute. Open, in that the code and models are released under the Mozilla Public License. Ubiquitous, in that the engine should run on many platforms and have bindings to many different languages.
The architecture of the engine was originally motivated by that presented in Deep Speech: Scaling up end-to-end speech recognition. However, the engine currently differs in many respects from the engine it was originally motivated by. The core of the engine is a recurrent neural network (RNN) trained to ingest speech spectrograms and generate English text transcriptions.
Let a single utterance \(x\) and label \(y\) be sampled from a training set
Each utterance, \(x^{(i)}\) is a time-series of length \(T^{(i)}\) where every time-slice is a vector of audio features, \(x^{(i)}_t\) where \(t=1,\ldots,T^{(i)}\). We use MFCC’s as our features; so \(x^{(i)}_{t,p}\) denotes the \(p\)-th MFCC feature in the audio frame at time \(t\). The goal of our RNN is to convert an input sequence \(x\) into a sequence of character probabilities for the transcription \(y\), with \(\hat{y}_t =\mathbb{P}(c_t \mid x)\), where for English \(c_t \in \{a,b,c, . . . , z, space, apostrophe, blank\}\). (The significance of \(blank\) will be explained below.)
Our RNN model is composed of \(5\) layers of hidden units. For an input \(x\), the hidden units at layer \(l\) are denoted \(h^{(l)}\) with the convention that \(h^{(0)}\) is the input. The first three layers are not recurrent. For the first layer, at each time \(t\), the output depends on the MFCC frame \(x_t\) along with a context of \(C\) frames on each side. (We use \(C = 9\) for our experiments.) The remaining non-recurrent layers operate on independent data for each time step. Thus, for each time \(t\), the first \(3\) layers are computed by:
where \(g(z) = \min\{\max\{0, z\}, 20\}\) is a clipped rectified-linear (ReLu) activation function and \(W^{(l)}\), \(b^{(l)}\) are the weight matrix and bias parameters for layer \(l\). The fourth layer is a recurrent layer [1]. This layer includes a set of hidden units with forward recurrence, \(h^{(f)}\):
Note that \(h^{(f)}\) must be computed sequentially from \(t = 1\) to \(t = T^{(i)}\) for the \(i\)-th utterance.
The fifth (non-recurrent) layer takes the forward units as inputs
The output layer is standard logits that correspond to the predicted character probabilities for each time slice \(t\) and character \(k\) in the alphabet:
Here \(b^{(6)}_k\) denotes the \(k\)-th bias and \((W^{(6)} h^{(5)}_t)_k\) the \(k\)-th element of the matrix product.
Once we have computed a prediction for \(\hat{y}_{t,k}\), we compute the CTC loss [2] \(\cal{L}(\hat{y}, y)\) to measure the error in prediction. (The CTC loss requires the \(blank\) above to indicate transitions between characters.) During training, we can evaluate the gradient \(\nabla \cal{L}(\hat{y}, y)\) with respect to the network outputs given the ground-truth character sequence \(y\). From this point, computing the gradient with respect to all of the model parameters may be done via back-propagation through the rest of the network. We use the Adam method for training [3].
The complete RNN model is illustrated in the figure below.